Geosynchronous Orbits are WEIRD
Geosynchronous Orbits are WEIRD with tags physics, minutephysics, science
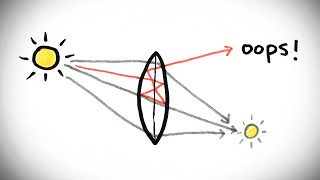
This video is about the physics of geosynchronous and geostationary orbits, why they exist, when they don't, when they're useful for communication/satellite TV, etc.
REFERENCES
Fraction of a sphere that's visible from a given distance
Orbital period
Kepler's third law
Kepler's 3rd law (which can be derived from Newton's law of gravitation and the centripetal force necessary for orbit as mr\omega^2=G\frac{mM}{r^2}, and using \omega=\frac{2\pi}{T}) is
T = 2pi Sqrt(r^3/(GM)) where M is the mass of the central object, G is the gravitational constant. Alternatively, we can solve for r, r = (T^2/(4pi^2) GM)^(1/3) ~ T^(2/3)/M^(1/3) = (T^2/M)^(1/3).
There is a limit (kind of like the Roche limit but for rotations). A rotating solid steel ball or other chunk of metal that has tensile strength (ie that isn't just a pile of stuff held together by gravity like most planets) would be able to spin faster.
Calculate how much of a planet's surface you can see from a given geosynchronous orbit/radius? (Obviously for lower ones you can see less, etc) - d/(2(R+d)) where d is distance to surface, ie, R is sphere radius, R+d is object radius from sphere center.
Let's plug that in with r being the geostationary orbit radius. That is, we have \frac{1}{2} \left(1- \left(\frac{4 \pi^2 R^3}{T^2 G M }\right)^{1/3}\right)
Average density of a sphere \rho is given by \rho =M/(\frac{4}{3}\pi R^3), ie \rho=\frac{3M}{4 \pi R^3} aka
\frac{M}{R^3}=\frac{4}{3}\pi \rho.
So we can convert the "fraction of planet surface seen" to
\frac{1}{2} \left(1- \left(\frac{3 \pi}{G \rho T^2}\right)^{1/3}\right)
So as either \rho or T\to \infty, the fraction goes to a maximum of \frac{1}{2}. And the point of "singularity" where the orbit coincides with the surface is where G\rho T^2=3\pi, aka \rho=\frac{3\pi}{GT^2}. For a rotation period of 3600s, that corresponds to a density \rho \approx 11000kg/m^3, which is roughly twice the density of the earth. For a rotation period of 5400s, we have \rho\approx 4800kg/m^3, which is basically the density of the earth.
Alternately, if we plug the density of the earth in to an orbit of period 5400s, we get as a fraction of the planet seen:
\frac{1}{2} \left(1- \left(\frac{3 \pi}{G \rho T^2}\right)^{1/3}\right) = 0.02
aka 2\% of the earth's surface.
MinutePhysics is on twitter - @minutephysics
Minute Physics provides an energetic and entertaining view of old and new problems in physics -- all in a minute!
Created by Henry Reich